对于当前新型合成毒品滥用的危害,上文中已根据相关资料从对个人、家庭、社会的危害方面进行了初步的分析,但具体的影响过程及影响程度往往难以做定量分析。为此,此次调查特设计家庭破裂、体质下降、记忆力下降、感染疾病、导致事故、对家庭成员的伤害、家庭的财产受到损失、诱发其他犯罪等11个指标来评估新型毒滥用的危害。采用的方法是因子分析方法。
基本原理与计算方法
在社会、政治、经济等领域的研究中,往往需要对多个变量进行观察,而在大多数的情况下,许多变量之间存在一定的相关关系,因而有可能用较少的综合指标分析存在于各变量中的各类信息,而各综合指标之间是彼此不相关的,代表各类信息的综合指标称为因子。因子分析法就是用少量几个因子来描述许多指标或因素之间的联系,以较少的几个因子反映原资料的大部分信息的统计学方法。
因子分析的特点
因子变量的数量远少于原有的指标变量的数量,对因子变量的分析能够减少分析中的计算工作量;因子变量不是对原始变量的取舍,而是根据原始变量等信息进行重新组构,能够反映原始变量大部分的信息;因子变量之间不存在线性相关关系,对变量的分析比较方便;因子变量具有命名解释性,即该变量是对某些原始变量信息的综合和反映。
其中,对多变量的平面数据进行最佳综合和简化,即在保证数据信息丢失最少的原则下,对高维变量空间进行降维处理。显然,在一个低维空间解释系统,要比在一个高维系统空间容易得多。英国统计学家摩瑟尔·斯格特1961年对英国157个城镇发展水平进行调查时,原始策略的变量有57个,而通过因子分析发现,只需要5个新的综合变量,就可以解释95%的原始信息。对问题的研究从57个维度降低到5个维度,因此可以进行更容易的分析。
最著名的因子分析研究,是美国统计学家斯通在1947年关于国民经济的研究,根据美国1927—1938年的数据,得到17个反映国民收入与支出的变量要素,经过因子分析,得到了3个新的变量,可以解释17个变量97.4%的信息。斯通将3个变量命名为总收入、总收入率、经济发展或衰退的趋势,对当代经济学的发展做出了卓越的贡献。
因子分析的应用
借助目前流行的统计软件SPSS,我们对各样本的11个指标进行主成分分析,通过主成分分析把指标之间的重叠信息过滤掉,具体计算过程如下:
第一步:采集数据。通过问卷调查,获得169个有效样本,经过数据录入与整理,得到新型合成毒品滥用后11个指标的数据。
第二步:对样本进行检验,看是否适合做主成分分析。这里我们采用KMO和巴特利球度检验(Bartlett's Test of Sphericity)检验法。检验结果如下:
表4-1 KMO和巴特利球度检验
| KMO取样适切性量数 | 0.725 | |
| 巴特利球度检验 | 近似卡方分配 | 356.648 |
| 自由度 | 96 | |
| 显著性(P值) | 0.000 | |
由表4-1得知,样本的KMO检验结果为0.725,超过0.7;巴特利球度检验的结果为356.648,值较大,应该拒绝零假设。综上可以看出,原样本适合做主成分分析。
第三步:构造因子变量,选取因子个数。我们运用SPSS,根据特征值的大小决定因子的取舍,这里把标准定为特征值大于1,即特征值大于1所对应的单位特征向量即为我们所提取的主因子。SPSS输出的结果如下:首先看碎石(图4-1):
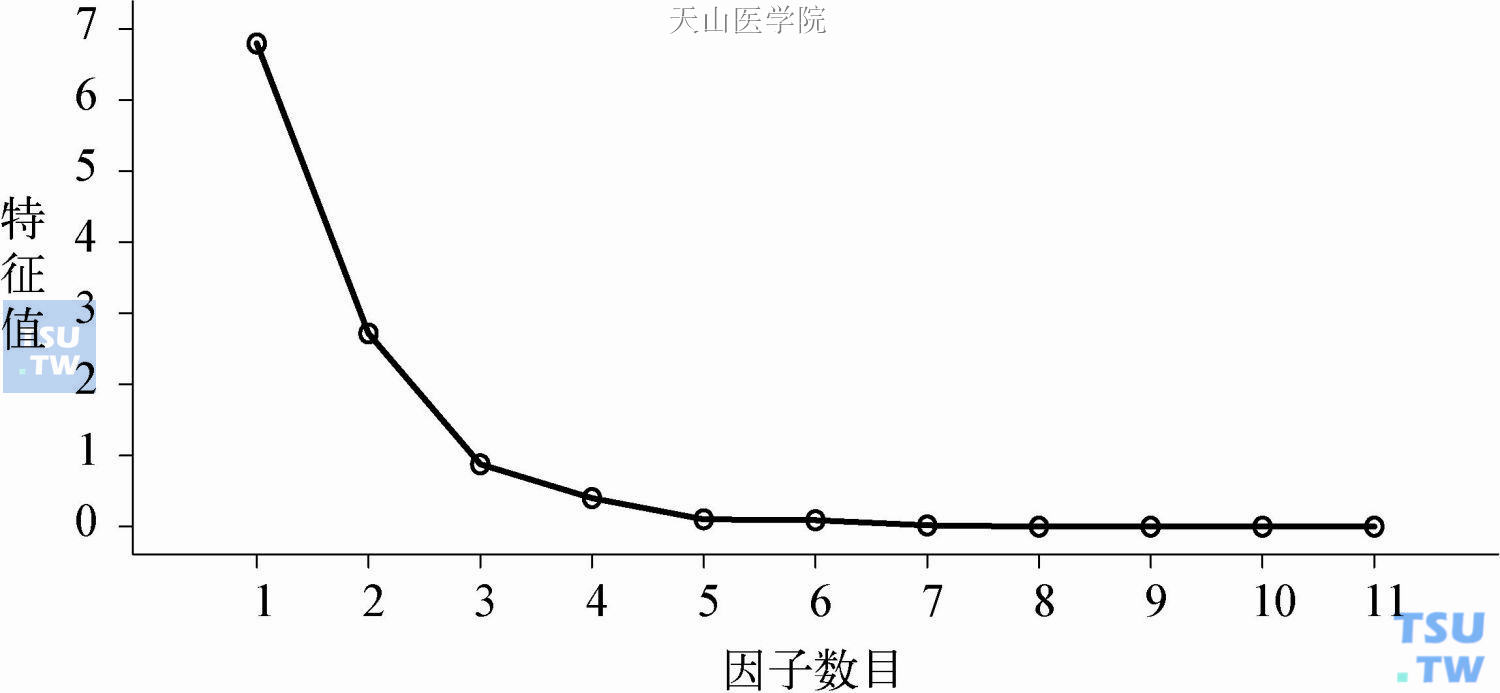
图4-1 因子的碎石图
在图4-1中,横坐标为因子数目,纵坐标为特征值。可以看到:第一个因子的特征值很高,对解释原有变量的贡献最大;第二个以后的因子特征值都较小,对解释原有变量的贡献很小,已经成为可以忽略的“高山脚下的碎石”,因此提取2个因子是合适的。其次再来看下面的因子载荷矩阵表:
表4-2 因子载荷矩阵总方差解释
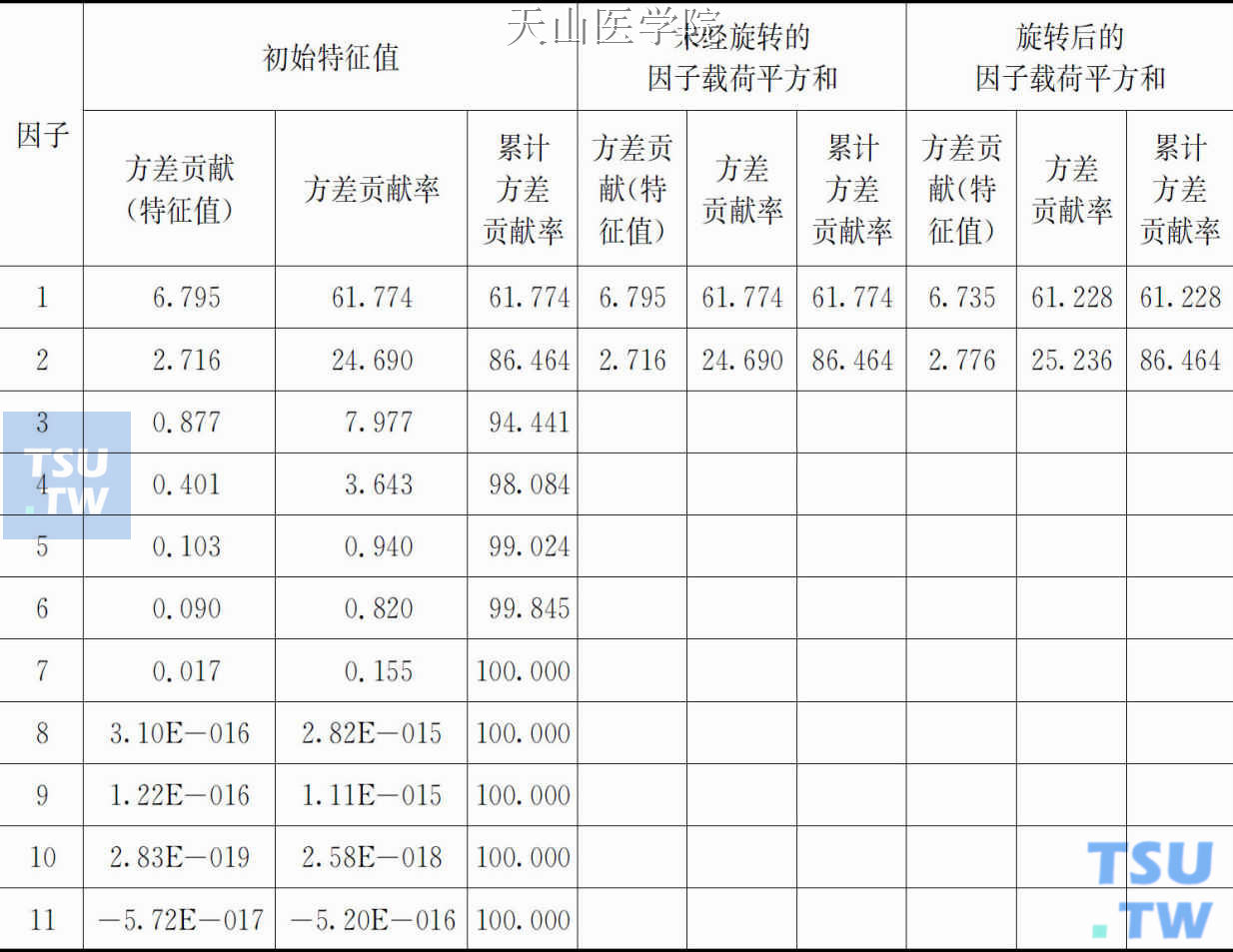
提取方法:主成分分析。
由表4-2可知,根据特征值大于1的标准,提取了2个主因子,累积方差达86.5%,即所提取的5个主成分能解释原11个变量的86.5%的信息。
第四步:旋转因子变量,使其更具有可解释性。旋转后的因子载荷矩阵如下:
表4-3 旋转后因子载荷矩阵
| 指标 | 主因子 | |
| 1 | 2 | |
| 记忆力严重下降 | 0.962 | 0.184 |
| 能够忘掉一切烦恼 | 0.200 | 0.882 |
| 心情非常愉快 | -0.090 | 0.841 |
| 自己的家庭破裂 | 0.397 | 0.777 |
| 自己流落社会 | 0.663 | -0.704 |
| 自己体质下降 | 0.962 | 0.184 |
| 自己感染疾病 | 0.949 | 0.034 |
| 导致事故 | 0.962 | 0.184 |
| 家庭财产受到重大损失 | 0.962 | 0.184 |
| 家庭成员身心受到严重伤害 | 0.934 | -0.006 |
| 其他违法犯罪 | 0.185 | -0.235 |
提取方法:主成分分析法。旋转方法:Kaiser正常化的方差最大旋转。转轴收敛于3个迭代。
由表4-3可知,在第一个因子上载荷超过0.7的有记忆力下降、体质下降、感染疾病、导致事故、财产损失、家庭成员受到伤害、其他违法犯罪共7个指标,所以这个因子表征了新型合成毒品滥用者个人身体与生产能力的诸多方面,在此将其命名为“个人身体与生产能力损害因子”;第二个因子上载荷超过0.7的有忘掉烦恼、心情愉快、家庭破裂、流落社会共4个指标,所以第二个因子表征了新型合成毒品滥用者心理、心情等受到的损伤,在此称为“心理能力损害因子”。
第五步:计算因子变量的得分。因子得分矩阵如下:
表4-4 因子得分矩阵
| 指标 | 主因子 | |
| 1 | 2 | |
| 记忆力严重下降 | 0.140 | 0.041 |
| 能够忘掉一切烦恼 | 0.007 | 0.316 |
| 心情非常愉快 | -0.036 | 0.309 |
| 自己的家庭破裂 | 0.039 | 0.273 |
| 自己流落社会 | 0.118 | -0.274 |
| 自己体质下降 | 0.140 | 0.041 |
| 自己感染疾病 | 0.142 | -0.013 |
| 导致事故 | 0.140 | 0.041 |
| 家庭财产受到重大损失 | 0.140 | 0.041 |
| 家庭成员身心受到严重伤害 | 0.141 | -0.027 |
| 其他违法犯罪 | 0.124 | -0.107 |
提取方法:主成分分析法。旋转方法:Kaiser正常化的方差最大旋转。因子得分。
根据因子得分矩阵表,可以得到如下因子得分模型:
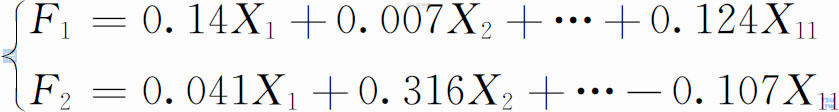
第六步:利用主成分计算各新型合成毒品对其滥用者的危害综合值。计算模型如下:

其中Ei为新型合成毒品滥用危害程度;
Wj(j=1,2)为各因子的权重,这里我们取各因子的方差贡献率作权重。
Fij(i=1,2,…,169;j=1,2)为各滥用者各因子的值。
计算过程如下表:
表4-5 各样本受新型合成毒品危害综合值排序表
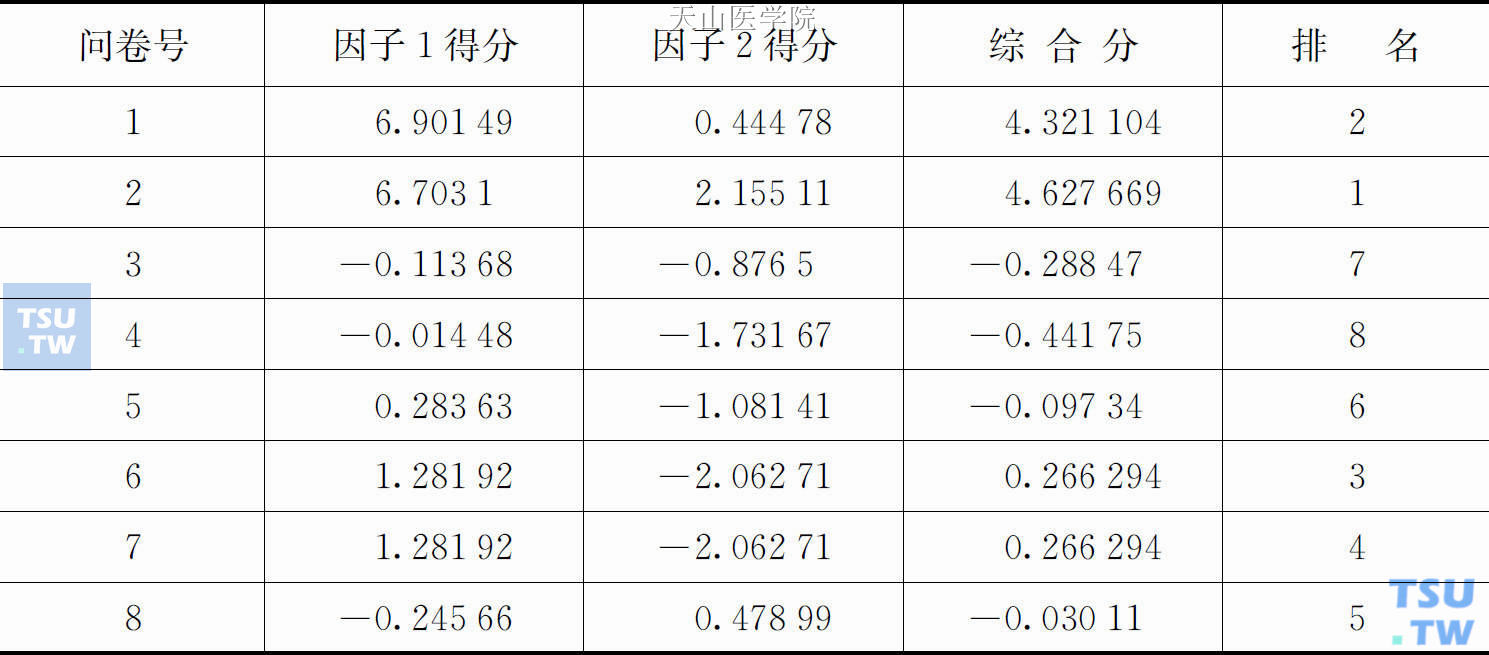
具体举例如计算问卷1这个样本的伤害程度则为:E1=F1×W1+F2×W2=0.61×6.90149+0.25×0.44478≈4.321104。在上述所举8个样本中,问卷号为2的样本受新型合成毒品的伤害程度最深,综合值为4.627669。为此,我们可以对每一个滥用新型合成毒品者的受危害程度进行综合评估,并借此采取有针对性的措施对相关个案进行剖析,对滥用者本人进行正确的帮教。
由上可知滥用新型合成毒品的危害主要表现在两个方面,其一是对滥用者身体能力、生产能力的危害;其二是对滥用者心理能力的危害。至于其对家庭、对社会的危害,都是从上述两种危害中衍生出来的。
因此,在对其进行预防教育或进行帮教时,不能因为新型合成毒品滥用者有偷盗、抢劫、故意伤害等行为,就认为其法律意识不强,因而要对其加强法律教育以期达到帮教的目的。而应该考虑到这一滥用者是否因身体已遭到严重损害而无法自我维持生存、心理上是否处于正常状态等,帮教的重点首先是想办法让滥用者身体与心理得到充分的调整与恢复。
可见,发现主因子对相关部门确定预防新型合成毒品滥用的重点方面及积极采取有针对性的措施救治或帮教新型合成毒品滥用者都起到十分重要的作用。一方面是在评估新型合成毒品滥用的危害时,最重要的两个评估指标就是滥用者身体生产能力、心理能力的损害程度,并可利用其计算新型合成毒品对滥用者的危害综合值。为此,我们可以对每一个滥用新型合成毒品者的受危害程度进行较为客观的综合评估。另一方面是要高度重视滥用者身体的康复治疗、心理治疗,相对而言,新型合成毒品滥用者心理的矫正更为关键,难度也更大;同时,培养滥用者专业技能是滥用者回归社会的重要手段。
