以上我们为简明起见,重点对超短脉冲激光的时间分布特性进行了描述。显然,实际当中任何激光脉冲的电场应该是同时包括时间和空间变量的时空分布函数,即E(![]() ,t)。当我们的观察或研究限定在某一特定的横向空间位置(x,y)时,则可以将激光脉冲的电场分布表示为时间t及传播方向z的函数,也就是E(t-z/c)。进一步而言,当z方向上位置也固定,即观察或研究被限制在特定的三维空间位置(x,y,z)时,才能得到仅含有时间变量的电场分布函数E(t)。前面我们提到,在真空中,光在一飞秒时间内向前传播0. 3μm。因此,一个脉宽为Δt的超短激光脉冲沿传播方向仅覆盖有限的空间尺度,用公式表示为Δz=cΔt。例如,脉宽为150飞秒的超短激光脉冲,沿传播方向的任一瞬间所具有的空间延伸为150×0. 3 = 45μm,而通常激光脉冲的光束直径一般为几个毫米量级。因此,形象地来看,在三维空间中一个实际飞秒激光脉冲是形如薄片的光子团。脉冲越短,这个由光子组成的薄片就越薄。
,t)。当我们的观察或研究限定在某一特定的横向空间位置(x,y)时,则可以将激光脉冲的电场分布表示为时间t及传播方向z的函数,也就是E(t-z/c)。进一步而言,当z方向上位置也固定,即观察或研究被限制在特定的三维空间位置(x,y,z)时,才能得到仅含有时间变量的电场分布函数E(t)。前面我们提到,在真空中,光在一飞秒时间内向前传播0. 3μm。因此,一个脉宽为Δt的超短激光脉冲沿传播方向仅覆盖有限的空间尺度,用公式表示为Δz=cΔt。例如,脉宽为150飞秒的超短激光脉冲,沿传播方向的任一瞬间所具有的空间延伸为150×0. 3 = 45μm,而通常激光脉冲的光束直径一般为几个毫米量级。因此,形象地来看,在三维空间中一个实际飞秒激光脉冲是形如薄片的光子团。脉冲越短,这个由光子组成的薄片就越薄。
与连续波激光的情形类似,超短脉冲激光也可以有三种典型的空间波前分布:平面波前、球面波前以及高斯型波前,其示意图如下图。平面波前只是理想化的波前,因为有限的波束尺寸及衍射效应的存在使激光能量不可能在无限大的空间范围内均匀分布;高斯波前在束腰处等同于有限的平面波前(下图c),随着传播距离的增大,高斯波前分布将和球面波前分布趋于一致。进一步增大传输距离,到达远场情况下,高斯波前分布或球面波前的局部又都可以用平面波前来近似。因此,高斯型波前分布是最常见的超短脉冲激光的空间分布形式。
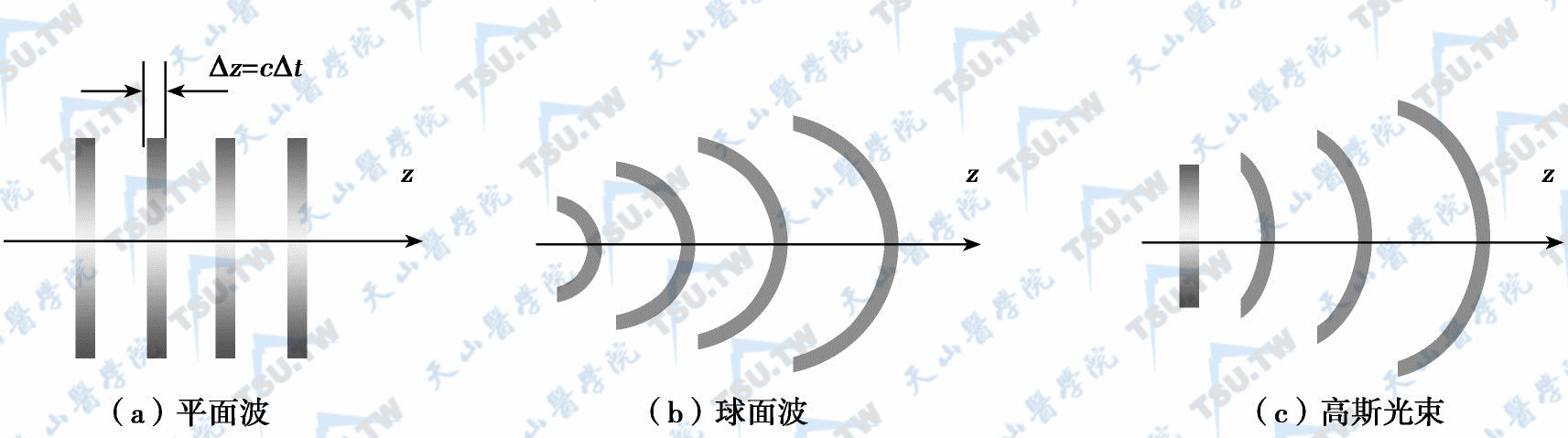
超短脉冲激光波前的空间分布形式(假设波由左向右传播时的侧视图)
对于大部分常见的高斯型超短脉冲激光而言,其光脉冲能量在与光传输方向垂直截面上的分布亦呈高斯型分布。这就是所谓的三维空间中的高斯脉冲的高斯光束。该光束相对传输光轴具有旋转对称性。当我们对脉冲光束的空间分布进行观测时,例如用一个屏幕来接收光脉冲,我们便自动地对其时间变化量进行了累积或平均。超短脉冲激光在空间中传输时,遵循与连续激光相同的规律(下图)。当脉冲光不是很强的情况下,在空间某一位置z处,光束半径w(z)的大小为:

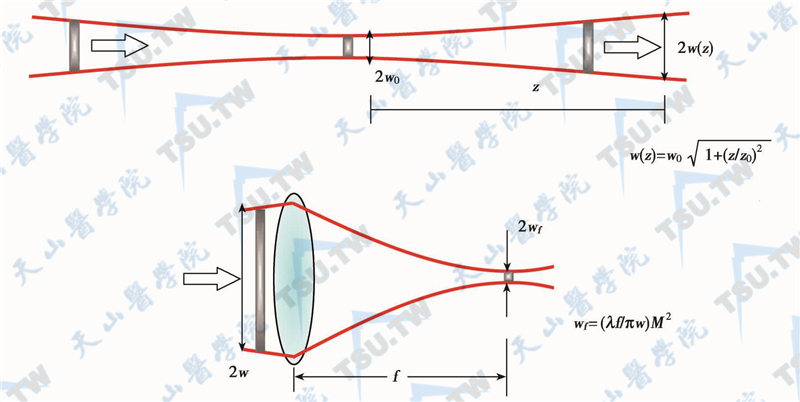
超短脉冲激光的空间传输和汇聚特性
式中,w0是光束束腰的(1/e2处)半径,![]() 是二分之一瑞利范围。瑞利范围代表了光束接近于准直的区域。显然,光束的束腰越大,其准直区(即接近平面波的区域)越长。在瑞利区的边缘(z=z0)处有
是二分之一瑞利范围。瑞利范围代表了光束接近于准直的区域。显然,光束的束腰越大,其准直区(即接近平面波的区域)越长。在瑞利区的边缘(z=z0)处有![]() 。
。
当光束被焦距为f的透镜汇聚时,其焦点处光斑的半径为:
![]()
式中,θw为光束的衍射发散角,w是入射到透镜上的接近准直的光束的半径。超短脉冲激光有与连续激光一样的衍射规律。光斑的尺寸越小,衍射角越大,即光束越发散。同时,发散角与波长成正比。严格地说,式(2. 7)仅适用于理想的基模高斯光束。在一般情况下,光束发散角的计算往往还需要乘上一个M2修正因子,即θw=(λ/πw0)M2。只有在理想情况下其M2才等于1。与连续或长脉冲激光一样,超短脉冲激光的M2值可以通过测量光斑大小和相应的光束发散角来得到。实际应用中,绝大多数飞秒激光光束的M2值在1和2之间。通常,飞秒激光器的制造厂商会提供所售激光系统输出光束的M2值。对任何激光束而言,M2值代表了激光束空间分布或可聚焦程度的质量评判参数。举例来说,假定一个入射飞秒激光脉冲的光斑半径为3mm、中心波长为1030nm、M2值为1. 3、聚焦物镜的焦距为3mm,则经透镜汇聚后焦点处的光斑大小为:
wf=M2(λ/πw)f=1. 3×1. 03μm×3mm/(3. 14×3mm)≈0. 43μm
需要注意的是,由于光的衍射过程具有明显的色散特征,而超短脉冲激光(特别是脉冲宽度小于20飞秒的激光脉冲)的光谱会非常宽,这意味着衍射会将脉冲中不同频率成分的光在空间上分开,从而造成脉冲的空间特性、频谱分布和时间特性间发生复杂的耦合。下图给出了在可见光波段的宽光谱光从微小的光纤孔径出射时由衍射色散引起的不同颜色的光在空间中发生分离的情况。虽然这更像是针对多波长连续光情况的小孔径衍射示意图,读者可以由此去设想类似情况下具有非常宽的光谱的超短脉冲激光的衍射情景。当超短脉冲激光的频谱在光斑不同空间位置上有所不同时,我们称之为具有空间啁啾的光脉冲。
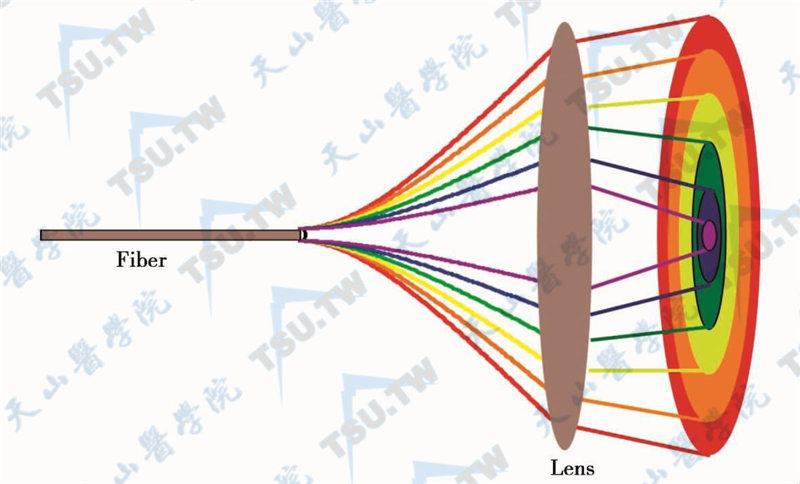
宽光谱的光通过小孔或小孔径出口衍射时所产生的不同颜色光空间分离现象。这种由衍射引起的空间色散效应对具有宽光谱的超短脉冲激光或飞秒激光而言有可能会非常明显
